

|
We live in a quantum universe. At a fundamental level, all physical systems are believed to be quantum mechanical. Quantum information science (QIS) concerns the characterization and utilization of intrinsically quantum properties of these physical systems. It has deep connections to several branches of science:
It provides the foundations for quantum computing, which uses quantum properties of physical systems to allow calculations that would be impossible with any conventional computer.
Applied to condensed matter theory, QIS allows us to understand quantum phases of matter which appear at low temperatures and cannot be characterized by any conventional order parameters.
In quantum gravity, spacetime itself can be understood as arising from the entanglement between some underlying degrees of freedom. Results from quantum information thus have implications for gravitational physics, even at the classical level.
QIS permeated by modern mathematics, including information theory, algebraic geometry, invariant theory, representation theory, and mathematical physics.
The Quantum Information Theory @UBC initiative complements other research efforts in quantum information and computation at UBC, in particular the Research Excellence Cluster for practical quantum computing, the QMI Grand Challenge Pushing the Boundaries of NISQ-era Quantum Computing, and the SFU-UBC collaboration on a quantum computer architecture based on silicon qubits and photonic interconnects. We are specifically interested in the following research fields:
Quantum phases of matter The experimental observation of the quantized Hall conductance in the early 1980's lead physics to realize that quantum Hall states belong to an unexplored class of exotic phases of fundamentally quantum nature. These so-called topological orders (Wen et al, Froehlich et al.) are inherently protected from local perturbations, making them excellent candidates for quantum memories and error correcting codes. Moreover, they support anyonic excitations, opening the path to topological quantum computation by braiding.
There is an explicit correspondence between quantum phases of matter and quantum computation, the so-called "computational phases of quantum matter". Namely, the computational power of resource states for measurement-based quantum computation is uniform across symmetry-protected phases of spin systems.
Quantum information in quantum gravity and quantum field theory One of the most exciting developments in theoretical physics over the past decade has been the realization that ideas from quantum information theory play a fundamental role in understanding the nature of spacetime and gravity. In our most complete models of quantum gravity, the geometry of spacetime is directly related to the structure of entanglement in the fundamental degrees of freedom. In some situations, even the Einstein equations which govern the dynamics of spacetime and its interactions with matter can be deduced directly from the physics of quantum entanglement!
Foundations of quantum computing Almost everything in the field of quantum computation boils down to two questions: "Can we build a quantum computer?"", and "What can we do with it?"". The second i s a question for theory, and it can be approached at three levels; the ad-hoc or short term level, the level of refinement of existing ideas, and the fundamental level. Here we are interested in the latter. The basic question we ask is: How can the quantum be used for computation?
The role of mathematics Theoretical physics has always inspired mathematicians and mathematics has provided essential tools to theoretical physics. Quantum information theory is no stranger to that intimate relationship. Knot invariants, which were confined to pure topology, are now used to classify quantum phases; models of quantum codes are based on braided tensor categories; propagation bounds in the spirit of partial differential equations are now essential tools to harness the power of locality in quantum information systems; convexity is a powerful principle when understanding entropic properties of quantum states and quantum channels; tensor networks both describe gapped ground states of matter and clarify the structure of big data sets; rigorous asymptotic analysis explains the attainability of scaling limits; SPT phases are classified by representation theory and K-theory. Quantum mechanics since its beginnings has profited enormously from mathematical methods and the mutual profit of mathematics and quantum information theory is enormous.
| extra space | ||||

|
extra space |
Sven Bachmann |
extra space |
I am interested in mathematical aspects of quantum mechanics, with a particular interest in condensed matter and many-body physics. Using methods of functional analysis and operator algebras, I have obtained novel results on the dynamics of quantum lattice systems as well as on exotic (topological) phases of matter. I have in particular proved the universality of quantization of the quantum Hall conductance. |
| extra space | ||||

|
extra space |
James Colliander |
extra space |
My research is mostly focused on rigorous understanding of the initial value problem for nonlinear Hamiltonian partial differential equations. The themes include low regularity well-posedness, maximal-in-time dynamics (global existence, singularity formation, soliton stability, symplectic nonsqueezing). The techniques involve harmonic analysis, dynamical systems, and symplectic geometry. |
| extra space | ||||

|
extra space |
Robert Raussendorf |
extra space |
My research interest is in quantum computation, in particular computational models, fault-tolerance, and the relation of quantum computation to foundations of quantum mechanics. I have invented the one-way quantum computer, a.k.a. measurement-based quantum computation (MBQC), jointly with Hans Briegel [PRL 86 (2001), UK patent GB 2382892, US patent 7,277,872]. |
| extra space | ||||

|
extra space |
Mark van Raamsdonk |
extra space |
In my research, I work towards a better theoretical understanding of elementary particle physics, classical and quantum gravity, and cosmology. Most of my research has focused on string theory, quantum field theory, and the remarkable equivalence between the two suggested by gauge theory/ gravity duality (a.k.a. the AdS/CFT correspondence). Currently, I am exploring connections between quantum information theory and quantum gravity. |
| extra space |

|
extra space |
Cihan Okay |
extra space |
My main motivation is to expand the scope of the long-standing interaction between topology and physics to the relatively young field of quantum information and computation. My work in algebraic topology has intersections with group cohomology, K-theory and simplicial homotopy theory. These structures find applications in quantum foundations such as contextuality of quantum mechanics. |
| extra space |

|
extra space |
Oleg Kabernik |
extra space |
I am interested in the notion of coarse-graining in quantum theory and how it relates to symmetries, dynamics and decoherence of quantum systems. In particular, I am working on an operational approach that implements coarse-graining using irreducible representations of operator algebras, and its extension that uses operator systems. Applications include: simplification and reduction of dynamics; control and protection of quantum information under operational constraints; decoherence and emergence of classicality in quantum systems. |
| extra space | ||||

|
extra space |
Michael Zurel Masters student Hennings, mzurel[at]gmail[dot]com |
extra space |
My research is primarily in the relation between quantum contextuality and quantum computation. I am also interested in classical simulation of quantum computation and in investigating and characterizing the resources required for quantum computation to exhibit a speedup over classical computation. |
| extra space |
Homotopical approach to quantum contextuality We extend Arkhipov's graph theoretic characterization of magic arrangements to arbitrary collection of contexts by relaxing the requirement that each observable belongs to exactly two contexts. We introduce the notion of a topological realization of a given set of operator constraints by cell complexes of algebraic topology. We prove that an arrangement is magic only if the first homotopy group (fundamental group) of any topological realization is non-trivial.
Magic arrangements are generalizations of Kochen-Specker type of contextuality proofs. In this form, the consistency conditions are expressed as a set of operator constraints given for each context. Operator solutions to these constraints are referred to as quantum realizations, and scalar solutions as classical realizations. Contextuality can be expressed as the non-existence of a classical solution, such cases are also referred to as magic arrangements.
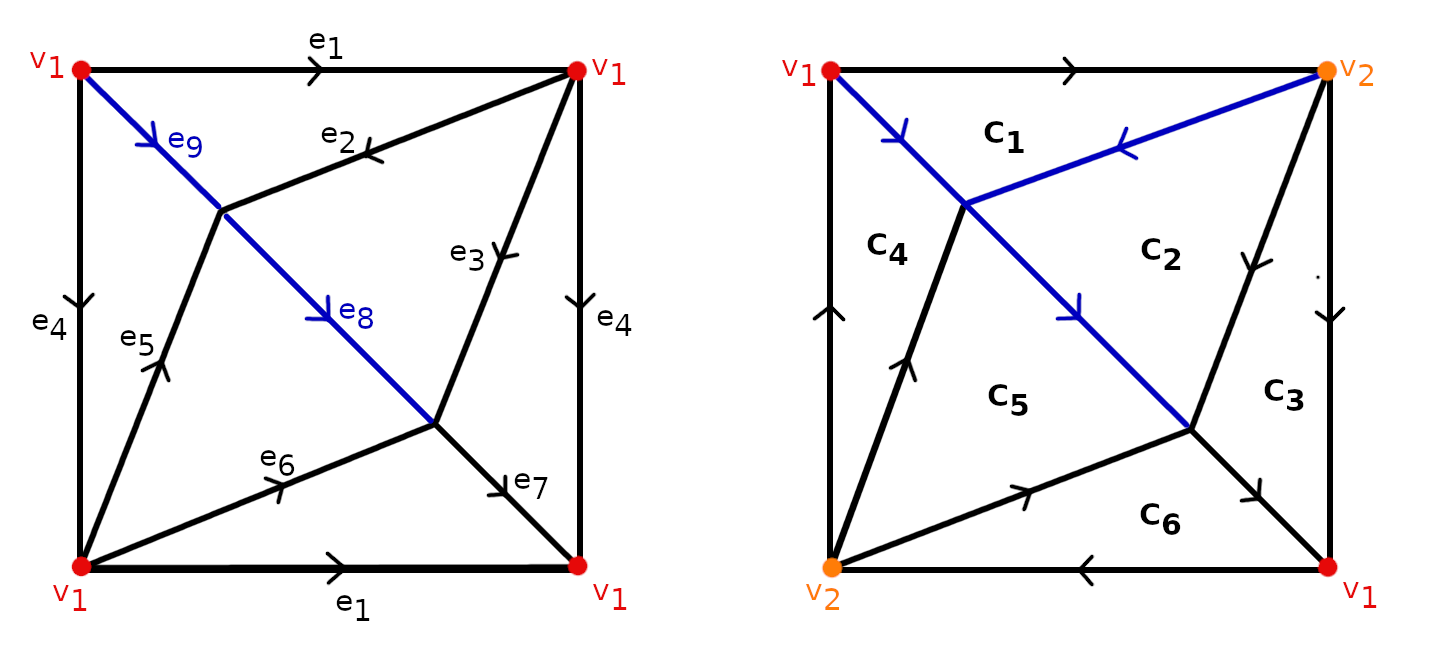
Arkhipov shows that an arrangement is magic if and only if its intersection graph is non-planar. Arkhipov's main tool in dealing with these type of constraints can only be applied when the observables belong exactly to two contexts and have eigenvalues +/-1. Our method applies to the general case of arbitrary contexts consisting of operators with eigenvalues a d-th root of unity. A topological realization is a 2-dimenisonal cell complex whose 1-cells (edges) are labeled by the operators and 2-cells (faces) are labeled by the contexts. In this case the fundamental group of the cell complex plays a crucial role in determining contextuality.
|
sp |
Topological realizations. We see two different topological realizations for the Mermin square. The boundary of the squares are identified with the indicated orientation to obtain a torus (left) and a real projective plane (right). In both cases edges are labeled by the operators of interest and triangles are labeled by the contexts. They both have non-trivial fundamental groups, and this can be seen as a witness for the contextuality of Mermin square. |
Journal References:
C. Okay, R. Raussendorf, Homotopical approach to quantum contextuality , arXiv:1905.03822 (2019).
More on topology of contextuality: C. Okay, D. Sheinbaum, Classifying space for quantum contextuality , arXiv:1905.07723.
A computationally universal phase of quantum matter [Published March 4, 2019] We provide the first example of a symmetry protected quantum phase that has universal computational power. This two-dimensional phase is protected by one-dimensional line-like symmetries that can be understood in terms of local symmetries of a tensor network. These local symmetries imply that every ground state in the phase is a universal resource for measurement based quantum computation.
In the presence of symmetry, quantum phases of matter can have computational power. The important property is that the computational power is uniform. It does not depend on the precise choice of the state within the phase, and is thus a property of the phase itself. In this way, phases of quantum matter acquire a computational characterization and computational value.
Quantum computational power of physical phases is utilized by measurement based quantum computation (MBQC), where the process of computation is driven by local measurements on an initial entangled state. Here, we consider initial states that originate from symmetry protected topological phases. Work on the usefulness of SPT phases of matter for MBQC have to date been focussed on spatial dimension 1. Computationally, physical phases in dimension 2 and higher are more interesting than in dimension 1. The reason is that, in MBQC, one spatial dimension plays the role of circuit model time. Therefore, MBQC in dimension D corresponds to the circuit model in dimension D-1, and universal MBQC is possible only in D >=2.
Here, we prove the existence of a computationally universal phase of quantum matter in spatial dimension two. The phase we consider is protected by one-dimensional line-like symmetries, generalizing the conventional notion of symmetry protected topological order defined by global on-site symmetries. As in the case of global symmetries, these line symmetries can be built from the local symmetries of a tensor network which persist throughout the phase. Using this, we establish that computational universality persists throughout the entire phase.
|
sp |
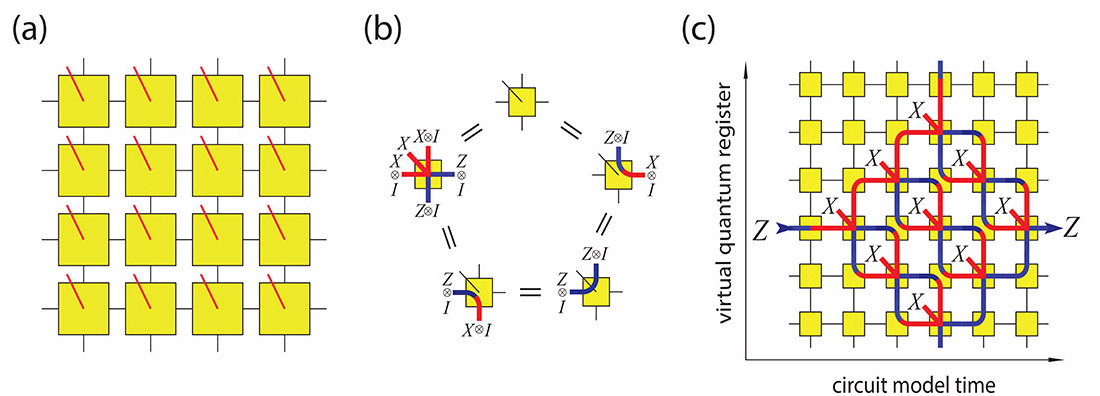
Symmetry Lego. Ground states throughout the whole cluster states have an enhanced symmetry, and the functioning of MBQC is based on it. This symmetry is best under stood in terms of tensor networks. (a) Tensor network representing an MBQC resource state in the 2D cluster phase. Every local tensor represents one physical spin 1/2 particle. (b) Throughout the cluster phase, each local tensor is invariant under a number of symmetries. These symmetries form the backbone of measurement-based computation in the cluster phase, as is illustrated in Fig. c. (c) The symmetries shown in (b) are composed into a larger pattern propagating a logical Z-operator forward in time. The area shown represents the ``clock cycle'' of the compution. If all physical qubits shown are measured in the X-eigenbasis, the resulting operation is the logical identity (computational wire), the simplest computational primitive. |
Journal References:
R. Raussendorf, C. Okay, D.S. Wang, D.T. Stephen, H. Poulsen Nautrup, A computationally universal quantum phase of matter, Phys. Rev. Lett. 122, 090501 (2019).
Further computationally universal SPT phases, and the connection to quantum cellular automata: D.T. Stephen, H.P Nautrup, J. Bermejo-Vega, J. Eisert, R. Raussendorf, Subsystem symmetries, quantum cellular automata, and computational phases of quantum matter, arXiv:1806.08780.